
 Share This Page
Share This Page| Home | | Mathematics | |  |  |  Share This Page Share This Page |
Copyright © 2013, Paul Lutus — Message Page
Version 1.3 (03.13.2014)
(double-click any word to see its definition)
Click here to download this article in PDF form

Compared to investing, there are few aspects of modern life in which innumeracy* has such severe consequences. One regularly hears horror stories in which people, highly motivated and with the best intentions, do exactly the wrong thing with their money.
It would be nice if people learned statistics and probability in school, but that's not a likely development. The result is that con men can persuade people of things that seem perfectly reasonable but that are false. Not just false, but diabolically false, false in ways that might separate you from your money.
Miracle Man
For example, did you know that a morally flexible stockbroker can send you market forecasts that accurately predict the direction of the stock market (up or down) in advance for months, without actually knowing anything about the real market or having psychic powers? In this article I'll explain how this scam works, and why it's so convincing.
The Contrarian
There's a philosophy among professional investors called "contrarianism" that says one should find out what other people are doing, and do the opposite. It's not as effective as actually knowing what's going to happen, but it's surprisingly effective. And for reasons given below and contrary to a carefully nurtured illusion, no one can really anticipate market changes, so being a contrarian is surprisingly effective.
Bad Timing
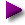
I know a woman whose parents lived through the Great Depression. About the time of the most recent market low point (Figure 2, "Slough of Despond"), she asked me for advice — should she liquidate her stock holdings to avoid more loss? I assured her the market would recover, that professionals were loading up on bargains, and she should be patient. Instead, about mid-March 2009, she panicked and sold everything. As Figure 2 shows, it was the worst possible moment to sell. She should have adopted the contrarian outlook, or simply done nothing. It was an example where reacting, being "prudent" and "taking control", was exactly the wrong thing to do.
Buy & Hold
This article describes what is demonstrably the most reliable, effective way to make money in stocks — simply, buy some stocks and sit on them. Don't listen to stockbrokers and investment counselors who try to persuade you they can increase your returns by actively managing your money — they can't, and the fact that they can't has been proven in a dozen different ways.
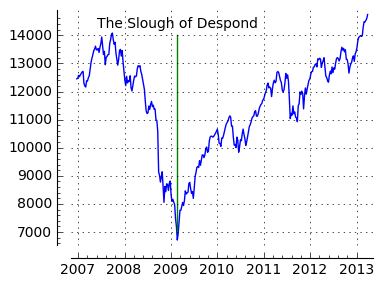
Buy & hold works because, even though the market fluctuates up and down in the short term, over months and years the average trend is upward (Figure 3). A buy & hold investor ignores short-term fluctuations and benefits from long-term market growth. Buy & hold investors also don't pay brokerage fees for services of doubtful value.
Market Model
This article includes an interactive stock market model to make some of its points. The reader can change the model's assumptions, test hypotheses, and get a sense of how equities markets work. One of the more important things the model shows is that a market with completely random movements, but an underlying long-term upward trend, favors the buy & hold investor over one with a managed portfolio.
The above are just a few of the points detailed in this article — things the professionals don't want you to find out. Read on — I describe a number of investor mistakes and how to avoid them.
Put simply, equities (or stocks) are a way for a business to raise operating capital. On one side of the transaction, a business has a product or an idea, but not enough money to develop it. On the other side, investors have money and are willing to invest in businesses and ideas that look promising. The investor accepts some risk in exchange for a share of possible profits.
Among possible investments and in the long term, equities are a rather good place to put your money, but there are some pitfalls. First, there are no guarantees, a stock portfolio doesn't come with an insurance policy, and at times the market can swing wildly, which scares some investors out of their wits. But notwithstanding short-term fluctuations, the long-term market grows in a reliable way (Figure 3), and investors who avoid certain behaviors do rather well for themselves.
But when you talk to market professionals, it's strongly suggested that you hire a professional money manager or investment counselor, on the ground that your life savings ought to be in the hands of someone who knows what he's doing. This article will examine that advice — does a stock market professional actually earn his fees?
Dartboard Contest
There's a persistent myth that, compared to acting on your own, hiring a stockbroker maximizes your chance to make wise, productive investments. This myth has been demolished so often that it's hard to believe anyone still accepts it. One of the more convincing refutations was the Wall Street Journal Dartboard Contest, which ran for a number of years. In the contest, an editor at the Wall Street Journal would pick a random selection of stocks (pictured as throwing darts at a list of stocks) and compare their performance against picks made by market professionals. Over the years, the contest's results clearly demonstrated that there was little difference between paying a stockbroker and throwing random darts.
In the game, the professionals had a small edge over throwing darts, an outcome that probably resulted from an announcement effect*. One announcement effect happens when eager investors find out what stocks the "experts" have picked and buy the same stocks, thus turning a prediction into a self-fulfilling prophecy. It is thought that, absent the announcement effect, the dartboard contest would have shown no advantage at all for the pros. It's important to add that if we include the effect of brokerage fees and the tax implications of frequent trades, the pros come out well behind the dartboard.
The Dartboard Contest is a clever example of an experiment that avoids asking unanswerable questions about whether "experts" can beat random stock picks in principle, and tests whether they can do it in fact. And ... they can't. There's no reliable evidence that paying a stockbroker to manage your portfolio actually increases your income enough even to make up for the broker's cost.
Chance and Probability
We all hear stories of investors who select stocks that grow and grow, eventually making them fabulously rich. Without any knowledge of probability, such stories seem to be about stock picking genius rather than chance. But, contrary to popular myth, the most likely explanation for such outcomes is simple chance — a random outcome, unpredictable in advance.
Because many of my readers don't have a deep understanding of probability, I offer this example of a random outcome. Let's say that an investor makes one market bet per week by flipping a fair coin:
That seems simple enough, and there are financial strategies available to accommodate such bets and predictions. Let's say for the sake of this game that the investor will double his money each week if the market agrees with his prediction, and will halve his money otherwise.
Now think about this — each week, by flipping a fair and random coin, the investor has a 50% chance to be right about the market direction, a 50% chance to double his money. And his choices are based on random coin flips — no experts, no market analysis, just chance:
No surprises so far. But when looked on as a sequence of events, the analysis is somewhat different. There's a simple probability equation that describes an investor's chance to produce an unbroken series of successful binary (i.e. yes/no) guesses:
(1) $p_n = 2^{-n}$Here are some sample results:Where $p_n$ = probability to have a continuous series of correct guesses lasting $n$ weeks.
What many people don't understand about these outcomes is that, even though the probability for a run of three correct guesses is $2^{-3}$ or $\frac{1}{8}$, the probability to guess correctly in any one of those tests remains $2^{-1}$ or $\frac{1}{2}$. The idea that a given guess owes something to its past or future is called the Gambler's Fallacy. Its relevance to the stock market lies in the fact that many people think because a stock is rising, depending on how they choose to think about it, it should continue to rise, or it should fall, because of what has happened in the past. That's fallacious thinking.
We can use equation (1) to compute the probability for any continuous run of correct guesses. Let's say for the sake of argument that choosing stocks is like flipping coins, and the choices are binary, meaning heads/tails, yes/no, up/down. Using this reasoning, the probability that an investor will be right twenty times in a row is $2^{-20} = \frac{1}{1,048,576}$. Not very likely.
So doesn't this mean that an investor with an admirable track record must possess investment genius, and that such an outcome cannot be explained by chance? No, not at all — any outcome can be explained by chance, and that explanation should always be considered. A small probability for individual success must necessarily be multiplied by the number of players, and there are millions of people playing the market, any of whom might succeed by chance. In detail:
| Population Size | Chance of runs of 20 correct guesses, with probability p = 2-20 (1/1,048,576)* |
|---|---|
| 10,000 | 0.95% |
| 100,000 | 9.10% |
| 1,000,000 | 61.47% |
| 5,000,000 | 99.15% |
| 10,000,000 | 99.99% |
Figure 4
I offer this analysis because of the number of times we hear people say, "They've been successful so long that their results can't be explained by chance." That is never true — any investment track record can be explained by chance. A careful study of probability shows that, as a population increases in size, individually improbable successes become more certain. It's equally certain that someone will try to say those successes resulted from genius, not chance.
Since we're on the topic of chance, I want to describe an incredibly devious, persuasive investment scam. Remember as you read what follows that there are any number of similar scams — I chose this one because it's totally convincing and easy to explain.
Don't read ahead! Think for a minute. Miracle Man has just mailed you a series of six completely correct market predictions, predictions that would have made you many millions of dollars if you had trusted him and moved your assets according to his instructions. His mailings arrived at the first of the month, and the market changes he predicted always took place after his mail arrived. His predictions aren't about particular stocks, but about the market as a whole. And he is always right.
You're an intelligent investor, you're skeptical of things that sound too good to be true, but Miracle Man sounds like the real deal. How could he be playing a trick? After all, his predictions arrive days or weeks before the changes he predicts, and he's correctly predicting the direction of the entire market. He must be the real thing. Right?
But before you sign your assets over to Miracle Man, I have to tell you that it's a scam, it's not real. In fact, the trick is so easy to perform that a computer can do it without human interference. Click here to find out how Miracle Man does it.

For a six-month program, Miracle Man ends up discarding most of the original addresses ($1-2^{-6}$ = 98.44%), but investors on the final list have been treated to a seemingly miraculous series of correct predictions, and unless they're very skeptical, they will be hot prospects.
Confronted by someone like Miracle Man, an intelligent, skeptical investor would ask some serious questions:The Efficient Market Hypothesis (EMH) is a theory describing ideal markets in which everyone has the same information, therefore no one has an inside track on profit — essentially, money flows to where it does the most good, thus maximizing efficiency, and everyone has the same chance to succeed.
In such an efficient market, there are no "secrets of the winners", and there are no legal ways to have an edge over other investors, so the only reliable way to make money is to ride the ascending market averages. Remember that, ignoring short-term fluctuations, the market gradually increases in value over years and decades (Figure 3), so one can assure a return by holding a cross-section of typical stocks and watching them increase in value.
Does the real equities market confirm the EMH? No one knows for sure. There is some evidence in favor of the idea. Most schemes to beat the market fail (like the dartboard contest described above), and many examples where someone gets ahead involve cheating — for example, by possessing "insider" information not available to everyone. Such activity is illegal, but that's not to say it doesn't happen.
There is one group who, when asked, will assure you that the EMH is false — stockbrokers and investment counselors, people whose livelihood depends on the notion that there are "secrets of the winners" that they understand and that you need to learn. But there is no evidence for the idea that there are reliably exploitable investment secrets, and plenty of evidence against this idea, like the dartboard contest described earlier.
Here's the bottom line — if the EMH is true, then no one can beat the market, and to try to beat the market by moving your assets around can only enrich the person who performs the moves for you — your stockbroker.
Here are typical arguments offered in favor of hiring a stockbroker or investment counselor:
Here are a seasoned investor's replies to the above points:
The buy & hold investment strategy is absurdly simple — an investor chooses a cross-section of reliable stocks, or invests in an index fund, a mutual fund that tracks a market indicator like the DJIA, and then sits on his investments. The basic idea of buy & hold is to avoid a strategy that involves buying and selling, because that activity costs money, and because the only reliable way to make money in stocks is to track long-term growth.
If a buy & hold portfolio is assembled correctly, there won't be any brokerage fees for the simple reason that there's no activity in the portfolio. If the assets are mutual index funds, there will be little or no management cost, because no management is expected or required.
Contrast buy & hold with an actively managed portfolio. An active portfolio typically costs the investor 2% per annum in brokerage and other fees, in a market that, in modern times, typically returns 6% per annum in profits (source). That means having a broker costs the investor about 1/3 of expected market returns, for a service that probably won't improve those returns.
Another argument against a managed portfolio is the fact that buying and selling equity assets triggers the realization of taxable capital gains and losses. Even if the net of capital gains and losses is neutral, it greatly increases the complexity of tax computation and filing, which means you'll be paying higher fees to another financial expert — a tax accountant.
The buy & hold idea isn't new or particularly controversial, except among stockbrokers, who think it's a terrible idea. But some heavyweights argue persuasively in favor of buy & hold — including Warren Buffett. In the Wikipedia buy & hold article, we read, "Others have advocated buy-and-hold on purely cost-based grounds, without resort to the EMH. Costs such as brokerage and bid/offer spread are incurred on all transactions, and buy-and-hold involves the fewest transactions for a given amount invested in the market, all other things being equal. Warren Buffett is an example of a buy-and-hold advocate who has rejected the EMH in his writings, and has built his fortune by investing in companies at times when they were undervalued."
I have to add that Buffett's enviable investment track record could easily result from a combination of chance and, more recently, a strong announcement effect, because everyone wants to invest in the same stocks Warren Buffett invests in.
Below you will find a live, interactive market model that uses computer simulation techniques to make some of the points made above with words. Here are some of the model's properties:
To change the model's parameters, enter different values in the green entry windows, then press Enter or press the "Compute" button to run the simulation with the new values. An increase in the number of investors or stocks will slow the simulator down, and on some browsers such a change may prevent the simulator from running at an acceptable speed.
In terms of speed and responsiveness, the best performers among browsers are Google Chrome and Firefox. The poorest performer is, as usual, Microsoft Internet Explorer.
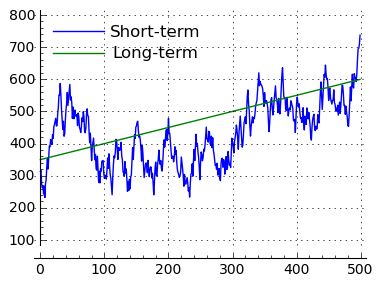
To fully appreciate the difference between the buy & hold strategy and a managed account, one must understand how compound interest works. Compound interest applies to an account in which accrued interest is added to the balance over time, which has a nonlinear amplifying effect (Figures 5 and 6). The equities market naturally compounds, and the trends shown in Figures 5 and 6 reflect outcomes for different average market growth rates.
A simple equation can be used to predict an annuity's future for a given periodic growth rate:
(2) $v_t = v_0\ e^{r t}$Where:
- $t$ = time periods in consistent units
- $r$ = periodic interest rate in units of $t$ (1% = 0.01)
- $v_0$ = account value at time zero
- $v_t$ = account value at time t
- $e$ = base of natural logarithms, i.e. 2.71828 ...
| Yearly Rate | 0 | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|
| 0.0% | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 1.0% | 1.00 | 1.11 | 1.22 | 1.35 | 1.49 | 1.65 |
| 2.0% | 1.00 | 1.22 | 1.49 | 1.82 | 2.23 | 2.72 |
| 3.0% | 1.00 | 1.35 | 1.82 | 2.46 | 3.32 | 4.48 |
| 4.0% | 1.00 | 1.49 | 2.23 | 3.32 | 4.95 | 7.39 |
| 5.0% | 1.00 | 1.65 | 2.72 | 4.48 | 7.39 | 12.18 |
| 6.0% | 1.00 | 1.82 | 3.32 | 6.05 | 11.02 | 20.09 |
| 7.0% | 1.00 | 2.01 | 4.06 | 8.17 | 16.44 | 33.12 |
| 8.0% | 1.00 | 2.23 | 4.95 | 11.02 | 24.53 | 54.60 |
| 9.0% | 1.00 | 2.46 | 6.05 | 14.88 | 36.60 | 90.02 |
| 10.0% | 1.00 | 2.72 | 7.39 | 20.09 | 54.60 | 148.41 |
For example, if we assume an average long-term 6% yearly growth rate, after 50 years the market will have grown to:
(3) $e^{r t} = e^{0.06 \times 50} = 20.09$
Or over 20 times its present size, and a buy & hold index fund that tracks the market as a whole can realize this growth rate. If we subtract a typical 2% brokerage fee burden, we instead would see:
(4) $e^{r t} = e^{0.04 \times 50} = 7.39$
Or only 36% of expected growth. This example is meant to alert investors to the deleterious effect of fees and other factors that eat into equity growth, and how those factors are amplified by compound interest.
Obviously if a broker could make up for added costs with added growth, then this sort of calculation would have no meaning. But all evidence suggests brokers can't do that.
On the general topic of compound interest, it is central to comprehending all financial matters, and it shows the importance of understanding mathematics. And whether you are yourself wealthy, want to become wealthy in the future, or want to take rich people outside and shoot them — for all these possibilities, you first need to understand how compound interest works.
Equities are a worthwhile investment. They're more risky than some other investments, but in modern times, the big risk of the market's alternatives is that they won't produce any growth. That possibility should always be included when evaluating investment risks — the risk that your money won't grow.
This article should make readers aware of the benefits of understanding a little mathematics. The central paradigm of modern financial activity is compound interest, and solving compound interest problems doesn't require an advanced mathematics degree.
Unless one understands a little mathematics, one will likely miss the most important advantage of a buy & hold strategy over a managed account, which is that a seemingly small annual percentage lost to brokerage fees every year will be amplified by compounding and greatly diminish one's portfolio value in the long term.
Thanks for reading.
| Home | | Mathematics | |  |  |  Share This Page Share This Page |